確率
試行と事象
Aの起きる確率P=事象Aの起きる場合の数/すべての場合の数
p(A) = n(A)/n(U)
同時確率
P(A∧B)=n(A∧B)/n(U)
条件付き確率
P(A∨B)=P(A∨B)/P(A)
乗法定理
P(A∨B)=P(A∨B)*P(A)
確率変数
確率分布・表
確率変数の平均値と分散
平均値 μ=E(X)
→期待値
分散 σ^2 = V(X)
→分散
連続な確率変数と確率密度関数
P(a<=X<=b)=∫[a,b]f(x)dx
累積分布関数
連続的確率変数の期待値と分散
平均値(期待値) μ = E(x) = ∫[a,b]xf(X)dx
分散 σ^2 = V(x) = ∫[a,b](x-μ)^2f(x)dx
標準偏差 σ = √σ^2
平均値は分布の重心位置
パーセント点とp値
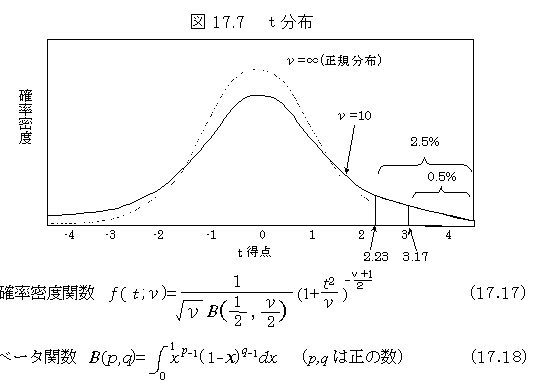
データ分析用語タ行
http://ifs.nog.cc/k-dai.hp.infoseek.co.jp/dai_01_bu/yougo-T.htm
上の図で言えば2.5%とあるのが両側5%点
100p%点とp値

確率変数の標準化

平均値や分散の異なる分布を平均0、分散1の標準的な分布に統一できる
0 件のコメント:
コメントを投稿