標本から得られる統計量def推定量
不偏分散と不偏性
ぶっちゃけこれではなんやかんやでわからない。
簡単に言うと,「(実際にはありえないが)何回も推定を繰り返すと,平均的には推定したい値 ![]() に合っている」というのが「不偏性」である。
に合っている」というのが「不偏性」である。
不偏性
http://case.f7.ems.okayama-u.ac.jp/statedu/lispstat-book/node106.html
これではっきりした。
私がもっとわかりやすく説明すると、母数θの周り(±的な意味で)にまんべんなく推定量がバラけているという状態。
その状態の時Tnは不偏性を持つというらしい(定義)
不偏分散はなぜn-1で割るのか
私的にはWikiの解説のほうがすんなり理解できた
不偏分散 の期待値が母分散
の期待値が母分散 に等しい事を示す。 以下、母平均を
に等しい事を示す。 以下、母平均を とし、
とし、 は
は から
から までの和を表す物とする。 また、関係式
までの和を表す物とする。 また、関係式
は繰り返し用いる。
分散 - Wikipedia
http://ja.wikipedia.org/wiki/%E5%88%86%E6%95%A3#.E4.B8.8D.E5.81.8F.E5.88.86.E6.95.A3.E3.81.AE.E6.9C.9F.E5.BE.85.E5.80.A4
手元の本には式ではなくて理屈を説明していたのでそちらも紹介する
そもそも分散の定義に於いて、平均との差を2乗するのには次の理由があった
このように単純に平均との差で分散を定義してしまうと常に分散は0になってしまう。
故に差を平方したものを足していくという定義をしたのだった。
ところで上の式に注目すると
X1からXn-1まで自由に数を与えることができるが、X1からXn-1まで定義してしまうとXnは自動的に決まってしまう。
この時の自由度はn-1になる。自由度が1小さくなった分散を求める分子の値は小さくなる。
故にn-1で割り、大きめに分散を見積る必要があると・・・
よく分からんw
こっちのほうが分かり良いかもよ
標本分散が母分散より少し小さくなる理由、不偏分散をn-1でわる理由 | OKWave
http://okwave.jp/qa/q4338548.html
(おまけ) イラストでわかる自由度と不偏分散
http://home.a02.itscom.net/coffee/tako08Annex2.html
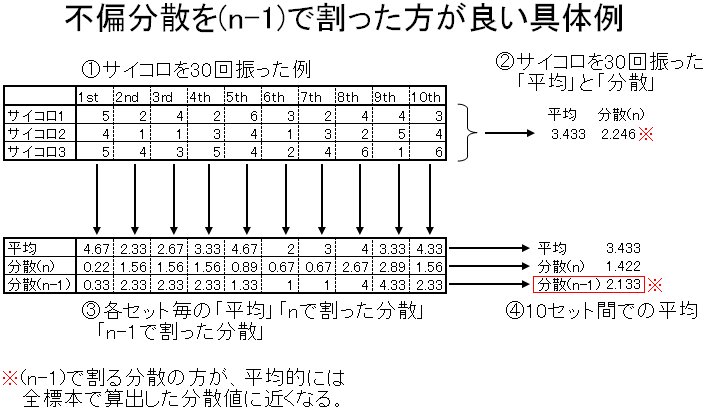
こんな画像があったので自分も実験して見ることにした。
ExcelVBAを用いることにした

標本数5
母集団の平均はR10C1(A10)←なぜOffice開発陣にはRC表記に統一しなかったのかと数時間問い詰めたいw
3.3
標本分散は2.31
個々の試行に対する平均はR6Cnに表示されている
個々の試行に対する平均の平均は3.3
個々の試行に対する標本分散の平均は1.95
個々の試行に対する不偏分散の平均は2.6
故に標本数5の段階でも、個々の試行に対する標本分散の平均は、母集団の標本分散よりも小さくなり、
個々の試行に対する不偏分散の平均のほうが母集団の標本分散に近くなることがわかる。

標本数10

標本数1000
手前味噌だが中々良い例を示せたと思う
![V[X]=E[X^{2}]-E[X]^{2},\,](http://upload.wikimedia.org/wikipedia/ja/math/7/7/f/77f85434ac3ccd00abbc274f6267d6f8.png)
![E[x_{i}]=\mu , \, V[x_i]=\sigma^{2}](http://upload.wikimedia.org/wikipedia/ja/math/5/7/e/57e7fdc7d3aa9e15a348d06f3226069d.png)
![\begin{align}E[u^{2}]&=E\left[ \frac{1}{n-1}\sum_{i} (x_{i}-\bar{x})^{2} \right] \\&=\frac{1}{n-1}\sum_{i}\left( E[x_{i}^{2}] -2 E[x_{i}\bar{x}] + E[\bar{x}^{2}] \right) \\ &=\frac{1}{n-1}\sum_{i}\left( \left(V \left[x_{i} \right]+E \left[x_{i}\right]^{2} \right) -2 E[\bar{x}^{2}] + E[\bar{x}^{2}] \right) \\ &=\frac{n}{n-1}\left( (\sigma^{2}+\mu^{2})- E[\bar{x}^{2}] \right) \\&=\frac{n}{n-1}\left( (\sigma^{2}+\mu^{2})-\left(V\left[\frac{1}{n}\sum_{i} x_{i}\right]+\mu^{2} \right )\right) \\&=\frac{n}{n-1}\left( (\sigma^{2}+\mu^{2})-\left(\frac{1}{n^{2}}\sum_{i} V\left[x_{i}\right]+\mu^{2} \right )\right) \\&=\frac{n}{n-1}\left( \sigma^{2}-\frac{1}{n^{2}} \cdot n\sigma^{2} \right) \\&=\sigma^{2}\end{align}](http://upload.wikimedia.org/wikipedia/ja/math/4/c/d/4cd8b1e45cc929b8b70fe6a3da18eacb.png)
0 件のコメント:
コメントを投稿